NOTE: I UPDATED ALL DOWNLOAD LINK
Hello again!
Remember i did a javascript version of the Tree Fractal(with the help of rosettacode)
So iv'e built another version in C#
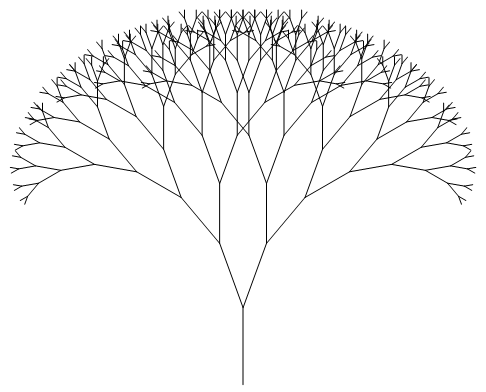
So here is the code:
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Windows.Forms;
namespace TreeFractal
{
public partial class Form1 : Form
{
static public Pen p = new Pen(Color.Black, 1);
static public Graphics g;
static public double deg_2_rad = Math.PI / 180.0;
static public float globalH;
static public float globalW;
static readonly object _locky = new object();
public Form1()
{
InitializeComponent();
}
private void drawTree(float x1, float y1, double angle, int depth, double angle1)
{
try
{
if (depth != 0)
{
float x2 = (float)(x1 + (Math.Cos(angle * deg_2_rad) * depth * 10.0));
float y2 = (float)(y1 + (Math.Sin(angle * deg_2_rad) * depth * 10.0));
lock (_locky)
{
this.Update();
p.Color = Color.FromArgb((depth * 255) % 16 * 14, (depth * 255) % 16 * 14, (depth * 255) % 128 * 2);
g.DrawLine(p, x1, y1, x2, y2);
}
drawTree(x2, y2, angle - angle1, depth - 1, angle1);
drawTree(x2, y2, angle + angle1, depth - 1, angle1);
}
}
catch (Exception ex)
{
MessageBox.Show(ex.ToString());
}
}
private void TreeCanvasLimits(float x1,float y1, double angle,int depth,double angle1)
{
if (depth != 0){
float x2 = (float)(x1 - (Math.Cos(angle * deg_2_rad) * depth * 10.0));
float y2 = (float)(y1 - (Math.Sin(angle * deg_2_rad) * depth * 10.0));
if (globalW > x2)
{
globalW = x2;
}
if(globalH < y2)
{
globalH = y2;
}
TreeCanvasLimits(x2, y2, angle - angle1, depth - 1,angle1);
TreeCanvasLimits(x2, y2, angle + angle1, depth - 1,angle1);
}
}
private void btnCreate_Click(object sender, EventArgs e)
{
g = this.CreateGraphics();
try
{
//globalH = 0;
//globalW = 0;
//TreeCanvasLimits(0, 0, -90.0, int.Parse(txtDep.Text), double.Parse(txtAngle.Text));
//this.Size = new Size((int)((globalW * (-2)) + 40), (int)((globalH + 60)));
g.Clear(Color.White);
drawTree((this.Width ) / 2, (this.Height - 150), -90.0, int.Parse(txtDep.Text), double.Parse(txtAngle.Text));
}
catch(Exception exx)
{
MessageBox.Show(exx.ToString());
}
}
private void btnLoop_Click(object sender, EventArgs e)
{
try
{
g = this.CreateGraphics();
g.Clear(Color.White);
for (int i = 0; i < 361; i++)
{
//g.Clear(Color.White);
//p.Color = Color.FromArgb((int)(i/4),(int)(i/3), (int)(i/2));
//MessageBox.Show("before " + i.ToString());
this.SuspendLayout();
drawTree((this.Width) / 2, (this.Height - 150), -90.0, 10, (double)i);
//System.Threading.Thread.Sleep(100);
this.ResumeLayout();
Application.DoEvents();
//MessageBox.Show("after " + i.ToString());
this.Update();
}
MessageBox.Show("Done");
}
catch (Exception ex)
{
MessageBox.Show(ex.ToString());
}
}
protected override void WndProc(ref Message m)
{
base.WndProc(ref m);
this.Update();
}
}
}
and here is a download link
Download The Project (rar file)
Download The Project (rar file)








